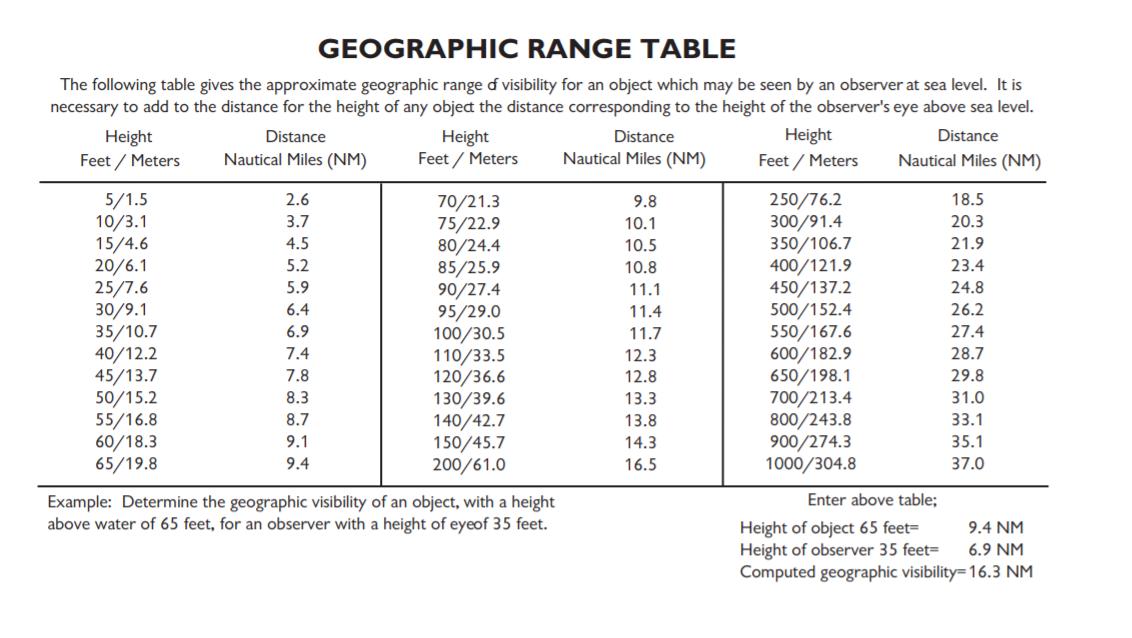
The table and equation are based on a spherical earth, especially when you look at the derivation of the equation.
The horizon distance (H) on a globe with radius (R) and observer height (X) can be accurately calculated with the right triangle rule. However this isn’t easy to work out in your head and it requires both the observer height and radius to use the same units.
H = [(R+X)^2 – R^2]^1/2
If we factor out the exponent
= [R^2 + 2*R*X + X^2 – R^2] ^1/2
The R^2 and -R^2 cancel each other out
= [2*R*X + X^2]^1/2
Pull the X out
= [(2*R + X) * X]^1/2
Which can be rewritten as
= (2*R + X)^1/2 * X^1/2
The format of this looks pretty similar to the equation posted by Z.W. Wolf. In the expression (2*R + X) ... Read even more